小型网站制作深圳seo优化排名软件
通信算法复习题
- 1、当信源发送信号满足以下哪一项条件时,接收端采用最小距离准则进行判决等价于采用最大后验概率准则进行判决?
- 2、OFDM系统的正交性体现在哪个方面?
- 3、模拟信号数字化过程中,哪一步会引入量化噪声?
- 4、OFDM系统中,由于时域信号波形累加会造成什么问题?
- 5、哪种滤波算法可以用于慢时变信道?
- 6、CDMA系统的下行信道一般采用什么扩频码?
- 7、LMS算法的步进因子取值范围?RLS算法的遗忘因子的取值范围?
- 8、CDMA系统中,扩频码的哪一项特性决定了系统多用户干扰水平的高低?
- 9、LMS算法的优势?
- 10、当随机过程满足什么条件时,可以认为该过程为均值遍历随机过程?
- 11、要能够应用维纳滤波,系统必须满足两个前提条件,线性系统和?
- 12、维纳霍夫方程的表达式。
- 13、随机过程的功率谱密度函数与该过程的什么函数互为傅立叶变换?
- 14、MMSE算法英文全称?其代价函数为?
- 15、n个线性无关向量构成的线性空间,其空间维度为多少?写出其一组正交基。
- 16、RLS算法中的因子λ的取值范围?
- 17、已知一个CDMA系统的信息比特速率是Rb,码片速率是Rp,求该CDMA系统的扩频增益。
- 18、CDMA系统的扩频码相关性作用。
- 19、维纳滤波的最优系数表达式。
- 20、两个矢量信号X=[x1,…,xN]T和Y=[y1,…,yN]T,N为矢量维度,其内积定义?当内积为零时,两个矢量什么关系?
- 21、影响无线信道性能的主要有两个因素?
- 22、采用OFDM技术的系统有(举1例),采用CDMA技术的系统有(举1例)
- 23、两个随机过程正交和不相关的关系?
- 24、OFDM系统的时频二维导频图案分布准则是什么?
- 25、模拟信号数字化过程中的量化误差由什么决定?
- 26、低阶调制和高阶调制的适用条件?
- 27、RLS算法和LS算法的代价函数是什么?区别在什么地方?
- 28、QPSK系统和16QAM系统星座图和接收符号判决区域?
- 29、什么是遍历随机过程?
- 30、采用维纳滤波的一次前向预测滤波器结构是什么?
- 31、五种滤波算法的比较(相同点,不同点,各自特性)。
- 31、最陡下降算法的原理,一维和二维迭代示意图。
- 32、AWGN信号的全称?其功率谱密度和自相关函数是什么?
- 33、CDMA系统的软切换和软容量原理。
- 34、QPSK和16QAM调制系统的框图。
- 35、OFDM系统的参数计算。
本复习题纲仅限于 CUIT 通信电子信息 刘大为 老师的通信算法
1、当信源发送信号满足以下哪一项条件时,接收端采用最小距离准则进行判决等价于采用最大后验概率准则进行判决?
当信源发送信号满足条件为 等概率分布 时
2、OFDM系统的正交性体现在哪个方面?
其正交性体现在其使用正交调制方法的方面,在ofdm系统中,频带被分为若干个独立的子载波,每个子载波都使用独立的正交调制方式进行正交调制,因此不同的子载波相互独立,没有任何互相干扰,这就保证了ofdm 系统的正交性,使得多个子载波就可以同时传输信息,从而不会产生干扰。时域,表现在一个 OFDM 符号时间 内,各个子载波都应该是整数周期的,另一个方面表现在频域,在频域,在某个子载波的频 率上,其他的子载波的频谱均为零。
3、模拟信号数字化过程中,哪一步会引入量化噪声?
量化的过程中会引入量化噪声,它决定了数字化信号的质量,在量化的过程中必须进行合理的参数设置,保证最佳的数字信号的质量。
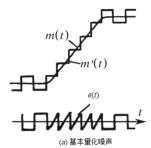
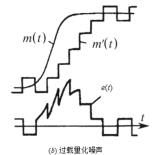
第一个原因是由于编码、译码时用阶梯波形去近似表示模拟信号波形,由于阶梯本身的电压突跳产生失真。如下图(a),这是增量调制的基本量化噪声,又称一般量化噪声。它伴随着信号永远存在,即只要有信号,就有这种噪声。
第二个原因是信号变化过快引起失真,这种失真称为过载量化噪声,见下图(b),它发生在输入信号斜率的绝对值过大时,由于当抽样频率和量化台阶一定时,阶梯波的最大可能斜率是一定的。若信号上升的斜率超过阶梯波的最大可能斜率,则阶梯波的上升速度赶不上信号的上升速度,就发生了过载量化噪声。
4、OFDM系统中,由于时域信号波形累加会造成什么问题?
卷积干扰:因为在这个系统中信号是同时在一个时间段内,因此会产生卷积干扰。
周期性冲突:当多个信号的波形相同时,在时域上的累加可能会导致周期性冲突效果。
5、哪种滤波算法可以用于慢时变信道?
RLS 算法用于慢时变信道(RLS属于广义Kalman滤波)。
移动平均滤波、Kalman滤波和Rauch-Tung-Striebel滤波都可以用于慢时变信道。
6、CDMA系统的下行信道一般采用什么扩频码?
WALSH码 (同步正交码),而在上行链路中,则采用 m码 进行扩频
7、LMS算法的步进因子取值范围?RLS算法的遗忘因子的取值范围?
LMS: 0 <μ < (2 / λmax) λmax 是相关矩阵R的最大特征值
LMS:通常是在0-1之间 lms 0.01-0.1
RLS:λ的范围为(0,1)[λ为遗忘因子]
RLS 为了保证算法的稳定性和有效性0.9-0.99之间
8、CDMA系统中,扩频码的哪一项特性决定了系统多用户干扰水平的高低?
互相关性
9、LMS算法的优势?
1、简单易实现
2、自适应性强、应用范围广
3、性能稳定
4、无需预知信号特性
10、当随机过程满足什么条件时,可以认为该过程为均值遍历随机过程?
通过一次观察估计一个随机过程的统计描述。设x 是一个时间离散的 WSS 随机过程:x的均值是 mx
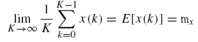
x 是均值遍历
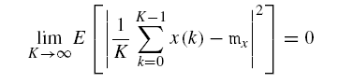
11、要能够应用维纳滤波,系统必须满足两个前提条件,线性系统和?
(1) 线性系统
(2) 广义宽平稳
12、维纳霍夫方程的表达式。
RCopt=P(最佳滤波器系数的判定)
其中R是自相关矩阵,要求R是满秩矩阵,P是期望输出与输入向量之间的互相关矢量
13、随机过程的功率谱密度函数与该过程的什么函数互为傅立叶变换?
自相关函数
14、MMSE算法英文全称?其代价函数为?
全称:Minimum Mean-Square Error
代价函数:J = E[(x - x_hat)^2] 或者 J=E[|e(k)|^2]
其中,x表示真实信号,x_hat表示估计信号
15、n个线性无关向量构成的线性空间,其空间维度为多少?写出其一组正交基。
N 维度
(1,0,0,…0)
(0,1,0,…0)
(0,0,1,…0)
(0,0,0,…1)
16、RLS算法中的因子λ的取值范围?
(0,1)
17、已知一个CDMA系统的信息比特速率是Rb,码片速率是Rp,求该CDMA系统的扩频增益。
CDMA扩频系统扩频增益定义为:码片速率/用户数据速率的结果取对数再乘10如语音的速率为9.6kbps,码片速率为1.228Mchips/s这样计算出来的扩频增益(也叫处理增益)的结果是21。
- G =10 * log(Rp/Rb)
如(10 * log(1228000/9600)= 21)
18、CDMA系统的扩频码相关性作用。
CDMA系统中的扩频码相关性可以提高系统的性能,它可以防止信号的干扰,并且可以确保系统中的信号不会互相干扰。
自相关性:区分用户,就像自己开机与基站取得联系时,只有自己与自己相关运算值最大。
互相关:决定了系统多用户干扰水平的高低,扩频码互相关性减少多用户的干扰
19、维纳滤波的最优系数表达式。
Copt = R-1P
其中R是自相关矩阵,要求R是满秩矩阵,P是期望输出与输入向量之间的互相关矢量
20、两个矢量信号X=[x1,…,xN]T和Y=[y1,…,yN]T,N为矢量维度,其内积定义?当内积为零时,两个矢量什么关系?
有两个相量:x=[x1;…;xI]T 和 y=[y1;…;yI]T
定义 <x;y>为内积:
<X,Y> = ||X|| ||Y|| cosθ
若<x,y>为实数, 则有:
||x|| 向量x的模或者长度
正交性: (X⊥Y)
如果<x,y>=0, 则他们间夹角为 90°
21、影响无线信道性能的主要有两个因素?
多径效应:产生频率衰落。
多普勒频移:产生时间性衰落。
22、采用OFDM技术的系统有(举1例),采用CDMA技术的系统有(举1例)
OFDM:ADSL 、Wi-Fi
CDMA:3G
23、两个随机过程正交和不相关的关系?
1.两个随机过程正交的意思是它们的互相关函数为0,这两个过程在统计意义上独立,不存在任何相关性。
2.而两个随机过程不相关的意思是它们的互协方差函数不为0,这两个过程在统计意义上存在相关性,即它们的变化不是独立的。
3.在通信系统中,总是力图按不相关或正交关系来设计在同一信道随机发送的二元或多元信号。对于多数通信信号以及噪声来说,基本上均值都为0,于是在实际应用中,不相关与正交没有本质区别。
24、OFDM系统的时频二维导频图案分布准则是什么?
OFDM系统的时频二维导频图案分布准则是最大可辨距离定理,其核心思想是尽可能地把发射系统的导频图案以最大可辨距离的方式分布在时频域上,以最大限度地抑制多径衰落。
时间导频 满足两个时间导频之间的距离小于相关时间,相关时间由多普勒频移决定。
频率导频 子载波之间的相干性是否一致,相邻的两个导频点之间的间距不能过大,过大导致导频点中间的内插点可信度降低,频率因素取决于多径。
25、模拟信号数字化过程中的量化误差由什么决定?
量化级数:量化级数越多,量化误差越小。
量化精度:量化精度越高,量化误差越小。
量化方案:不同的量化方案对于相同的量化级数和精度,其量化误差也会不同
26、低阶调制和高阶调制的适用条件?
低阶调制适用于信道信噪比较低的情况
高阶调制适用于信道信噪比较高的情况
因为高阶调制带来更好的频谱效率,所以一旦信道环境比较好,就可以切换到高阶调制上增加信息传输速度。很明显,在信道环境不那么好的场合,应该用低阶调制。
高阶调制抗干扰的能力远远小于低阶调制。就算是5G网络下,只有在干扰小的时候,才会使用256QAM的调制方式,而在干扰大、无线环境差(比如房间深处)时,基站会自动的选择更低阶的调制方式,来使得数据能够顺利传输,也就是说,此时数据传输速率会大大降低。
27、RLS算法和LS算法的代价函数是什么?区别在什么地方?
RLS算法的代价函数为
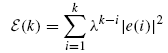
LS算法的代价函数为
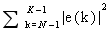
但RLS算法具有较快的收敛速度和较好的稳定性,并且具有自适应的优点。
RLS算法使用了递推的形式来更新系数,可以实现对系数的在线估计
28、QPSK系统和16QAM系统星座图和接收符号判决区域?
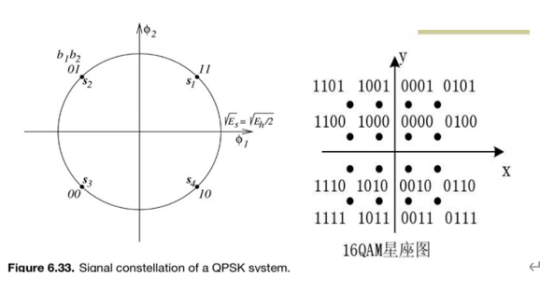
QPSK系统的星座图是一个四角星,它的接收符号判决区域是四个等分的正方形。每一个符号代表二进制中两个数字的状态。
16QAM系统的星座图是一个16个点的星座图,接收符号判决区域是4x4的网格。每一个符号代表四位二进制数字的状态。
29、什么是遍历随机过程?
遍历性:遍历性又称各态历经性,信号的任何一个样本函数的时间平均等于它的统计平均。
本质:用时间平均代替统计平均
30、采用维纳滤波的一次前向预测滤波器结构是什么?
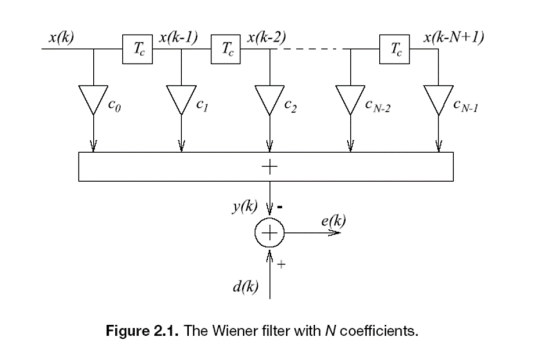
31、五种滤波算法的比较(相同点,不同点,各自特性)。
相同点:
所有五种滤波算法都是对信号进行预测和估计的算法。
它们都是用于从信号中去除噪声和干扰的工具。
不同点:
最小二乘滤波是一种简单的算法,用于预测和估计信号。
卡尔曼滤波是一种动态系统模型的滤波算法,用于处理含有连续噪声的信号。
递推最小二乘滤波是卡尔曼滤波的变体,专门用于快速预测和估计信号。
维纳滤波是一种最优滤波算法,适用于预测带有随机误差的信号。
快速傅里叶变换是一种基于傅里叶变换的滤波算法,可以在频域中对信号进行处理。
特性:
最小二乘滤波的特性是简单实用,但需要满足相关关系和线性性。
卡尔曼滤波的特性是具有自适应性和鲁棒性,但需要对动态
限幅滤波法
优点:能有效克服因偶然因素引起的脉冲干扰。
缺点:无法抑制那种周期性的干扰平滑度差。
算数平均滤波
优点:对滤除混杂在被测信号上的随机干扰信号非常有效。
缺点:不易消除脉冲干扰引起的误差。
滑动平均滤波法
优点:对周期性干扰有良好的抑制作用,平滑度高适用于高频振荡的系统。
缺点:灵敏度低。
加权递推平均滤波法
优点:适用于有较大纯滞后时间常数的对象和采样周期较短的系统。
缺点:对于纯滞后时间常数较小,采样周期较长。
限幅平均滤波法
B、优点:融合了限幅滤波法递推平均滤波法的优点,对于偶然出现的脉冲性干扰,可消除由于脉冲干扰所引起的采样值偏差。
C、缺点:实现复杂。
31、最陡下降算法的原理,一维和二维迭代示意图。
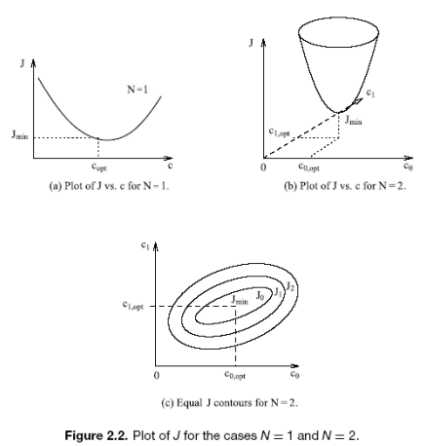
其原理是通过在状态空间上搜索最优解,使得对应的代价函数值得到最大减少。
一维最陡下降算法的迭代示意图如下:在数轴上,选择一个初始点,并从该点开始向下搜索,每次移动到当前位置的梯度方向,直到代价函数的值不再下降。
二维最陡下降算法的迭代示意图如下:在平面直角坐标系中,选择一个初始点,并从该点开始向下搜索,每次移动到当前位置的梯度方向,直到代价函数的值不再下降。
32、AWGN信号的全称?其功率谱密度和自相关函数是什么?
AWGN代表的是高斯白噪声(Additive White Gaussian Noise)
其功率谱密度是常数,表示噪声功率分布均匀,不存在任何频率偏移。
自相关函数是高斯型函数,表示噪声在时间上的相关性很弱,与其他时间点相关程度随着时间差的增加而逐渐减小。
功率谱密度:
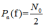
自相关函数:
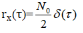
图像:
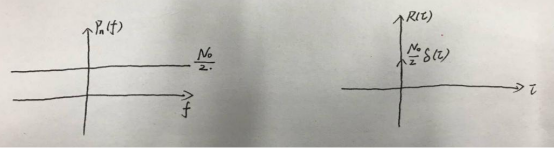
33、CDMA系统的软切换和软容量原理。
1.软切换
所谓软切换是指移动台需要切换时,先与新的基站连通再与原基站切断联系,而不是先切断与原基站的联系再与新的基站连通。软切换只能在同一频率的信道间进行,因此,模拟系统、TDMA系统不具有这种功能。软切换可以有效地提高切换的可靠性,大大减少切换造成的掉话,因为据统计,模拟系统、TDMA系统无线信道上的掉话90%发生在切换中。
2.软容量:
在FDMA、TDMA系统中,当小区服务的用户数达到最大信道数,已满载的系统再无法增添一个信号,此时若有新的呼叫,该用户只能听到忙音。而在CDMA系统中,用户数目和服务质量之间可以相互折中,灵活确定。例如系统运营者可以在话务量高峰期将某些参数进行调整,例如可以将目标误帧率稍稍提高,从而增加可用信道数。同时,在相邻小区的负荷较轻时,本小区受到的干扰较小,容量就可以适当增加。
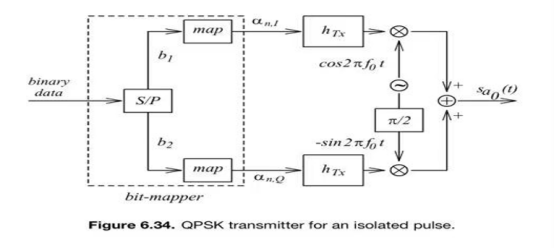
34、QPSK和16QAM调制系统的框图。
-
(QPSK 调制框图)
-
(QPSK 调制解调系统框图) 推荐这个
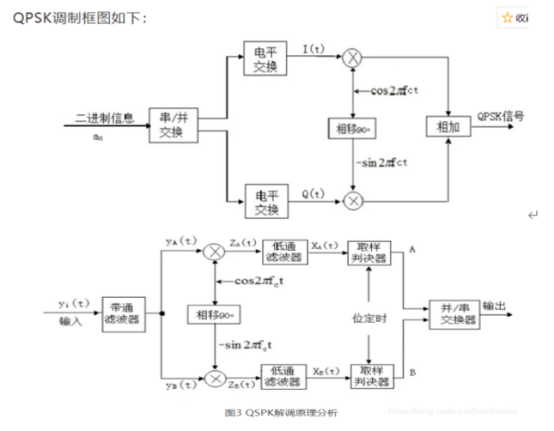
-
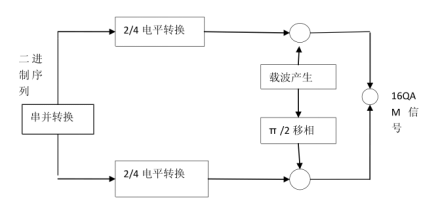
(16QAM调制框图)
- (任意M进制MQAM解调框图)
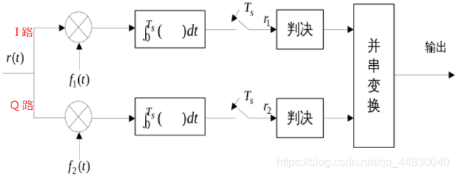
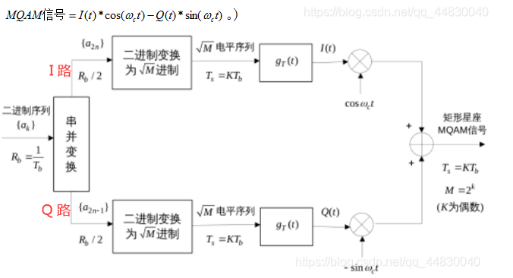
- (任意M进制MQAM调制框图)
35、OFDM系统的参数计算。
关键参数:系统带宽、比特率、保护时延、符号长度、子载波带宽、FFT点数
例如:已知OFDM系统,系统带宽15MHz,路径时延(rms)200ns,数据传输速率(比特率)20Mbps。求:FFT点数,调制类型及子载波传输速率。
步骤:
1.路径时延决定保护时延Tg:保护时延=2~4倍路径时延,题目会给出具体倍数。
2.符号长度TS是保护时延的4~5倍,题目会给出具体倍数。
(TS=Tg+TFFT Ts:符号长度 Tg:保护时延 TFFT:信息长度,用于FFT计算的时间长度)
3.子载波带宽是信息长度的倒数。
4.FFT点数应该是2M,由N(系统带宽/子载波带宽)决定(2M>= N).
5.调制类型由传输速率计算得出.
解:
1、确定保护时延:Tg=4rms=800ns
2、计算符号长度:Ts=6800ns=4.8us
3、计算信息长度:TFFT=Ts-Tg=4us
4、计算子载波带宽=1/TFFT=1/4us=250kHz
5、计算FFT点数(FFT点数2M>=N):N=系统带宽/子载波带宽=15MHz/250KHz=60, 故选择64阶
6、每个子载波的速率应该大于数据传输速率/N:20M/64=312.5kb/s,于是每个符号携带的信息量为:子载波传输速率符号长度=312.50.0048=1.5bit(于是每个符号携带信息量至少为2bit)
7、如果考虑纠错编码(1/2码率),调制类型应该选16QAM。(16QAM中,一个符号带4bit:24)
