自建网站系统哪些网站是营销型网站
参考效果
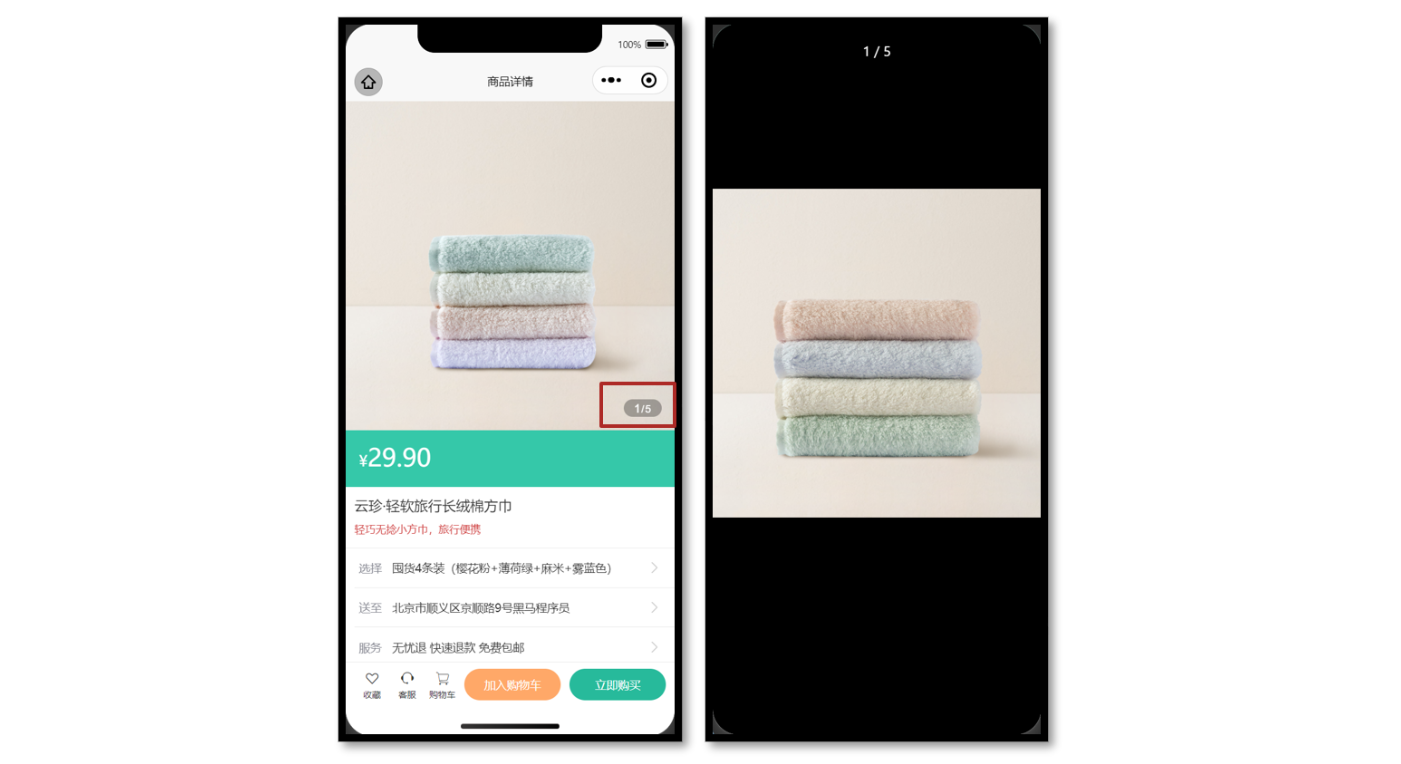
当轮播图滑动切换的时候更新自定义下标,当图片被点击的时候大图预览。
参考代码
商品详情页轮播图交互
<script setup lang="ts">
// 轮播图变化时
const currentIndex = ref(0)
const onChange: UniHelper.SwiperOnChange = (ev) => {currentIndex.value = ev.detail.current
}// 点击图片时
const onTapImage = (url: string) => {// 大图预览方法uni.previewImage({current: url, //图片路径urls: goods.value!.mainPictures, //预览图片列表})
}
</script><template><!-- 商品主图 --><view class="preview"><swiper @change="onChange" circular><swiper-item v-for="item in goods?.mainPictures" :key="item"><image @tap="onTapImage(item)" mode="aspectFill" :src="item" /></swiper-item></swiper><view class="indicator"><text class="current">{{ currentIndex + 1 }}</text><text class="split">/</text><text class="total">{{ goods?.mainPictures.length }}</text></view></view>
</template>
