1.网络安全常识及术语
下边基于这次攻击演示我们介绍一下网络安全的一些常识和术语。
资产
任何对组织业务具有价值的信息资产,包括计算机硬件、通信设施、 IT 环境、数据库、软件、文档资料、信息服务和人员等。
网络安全
网络安全是指网络系统的硬件、软件及其系统中的数据受到保护,不因偶然的或者恶意的原因而遭到破坏、更改、泄露,系统连续可靠正常地运行,网络服务不中断的状态。从广义上说,网络安全包括网络硬件资源及信息资源的安全性。从用户角度看,网络安全主要是保障个人数据或企业的信息在网络中的机密性、完整性、可用性,防止信息的泄漏和破坏,防止信息资源的非授权访问。对于网络管理者来说,网络安全的主要任务是保障合法用户正常使用网络资源,避免病毒、拒绝服
务、远程控制、非授权访问等安全威胁,及时发现安全漏洞,制止攻击行为等。从教育和意识形态
方面,网络安全主要是保障信息内容的合法与健康,控制含不良内容的信息在网络中的传播。
网络空间(Cyberspace)
是一种包含互联网、通信网、物联网、工控网等信息基础设施 , 并由人 -机- 物相互作用而形成的动态虚拟空间。网络空间安全既涵盖包括人、机、物等实体在内的基础设施安全, 也涉及到其中产生、处理、传输、存储的各种信息数据的安全。随着云计算、大数据、物联网、量子计算等新兴技术的迅猛发展, 网络空间安全面临着一系列新的威胁和挑战。例如 2018 年 3 月 17 日,英国《卫报》爆出英国的数据分析公司 Cambridge Analytica (剑桥数据分析)在美国大选中为川普服务。网络空间安全问题的影响力不再局限于数据篡改、系统控制和信息泄露等「狭义」网络安全问题,真实世界和社会的行为可以被来自其「数字孪生」世界的特定组织所操控。备受追捧的特斯拉电动汽车自动驾驶功能是另一例真实世界和「数字孪生世界」直连的案例,在这个案例里,特斯拉借助云计算、人工智能技术使得无人驾驶成为一项颇具吸引力的卖点,但该功能自诞生以来屡次被曝光多种类型的网络安全漏洞,这些漏洞一旦被攻击者利用,轻则使车辆迷失路线,重则造成驾驶失控、车毁人亡。我们的真实世界正在经历的各种数字化转型、升级和联网浪潮,不仅仅需要大数据、人工智能、云计算、5G 等这些新技术的持续推动力,更离不开网络安全技术在每一项新技术背后的保护力加持。没有网络安全的基础保障,网络空间安全无从谈起。
漏洞
上边提到的 “ 永恒之蓝 ” 就是 windows 系统的漏洞
漏洞又被称为脆弱性或弱点( Weakness ),是指信息资产及其安全措施在安全方面的不足和弱
点。漏洞一旦被利用,即会对资产造成影响。通常一个网络的漏洞 / 弱点可被分为:技术漏洞、配
置漏洞和安全策略漏洞。
0day
是指负责应用程序的程序员或供应商所未知的软件缺陷,尚未公开的漏洞。永恒之蓝在没有被公开
前就是 0day 。
1day
刚被官方公布的漏洞就是 1day ,刚被公布得了漏洞会有一个打补丁的时间差,这个时间差可以被黑客所利用。
后门
后门是一种用于获得对程序或在线服务访问权限的秘密方式。一般是绕过安全控制而获取对程序或
系统访问权的方法。上边的meterPeter 就是一种后门程序。我们可以用它很方便的进行目标系统的访问。
exploit
exploit ,指的是漏洞利用程序,我们在上面敲的 exploit 的命令就是执行永恒之蓝的漏洞利用程序来攻击目标win7 。
它在黑客眼里就是漏洞利用。有漏洞不一定就有 Exploit (利用 ) ,有 Exploit 就肯定有漏洞。
我们几乎每隔几天就能听到最近有一个新发现的可以被利用( exploit )的漏洞( vulnerability ),然后给这个漏洞打上补丁。而事实上,这里面的内容比你想象的要多,因为你不可能知道所有软件的漏洞,而且那些可利用的漏洞也只是被少数人所了解。漏洞是存在于一个程序、算法或者协议中的错误,可能带来一定的安全问题。但不是所有的漏洞都是能够被利用来攻击(exploitable )的,理论上存在的漏洞,并不代表这个漏洞足以让攻击者去威胁你的系统。一个漏洞不能攻击一个系统,并不代表两个或多个漏洞组合就不能攻击一个系统。例如:空指针对象引用(null-pointer dereferencing )漏洞可以导致系统崩溃(如果想做拒绝服务攻击就足够了),但是如果组合另外一个漏洞,将空指针指向一个你存放数据的地址并执行,那么你可能就利用此来控制这个系统了。
一个利用程序 (An exploit) 就是一段通过触发一个漏洞(或者几个漏洞)进而控制目标系统的代码。攻击代码通常会释放攻击载荷(payload ),里面包含了攻击者想要执行的代码。 exploits 利用代码可以在本地也可在远程进行。一个远程攻击利用允许攻击者远程操纵计算机,理想状态下能够执行任意代码。远程攻击对攻击者非常重 要,因为攻击者可以远程控制他/ 她的主机,不需要通过其它手段(让受害者访问网站,点击一个可执行文件,打开一个邮件附件等等),而本地攻击一般都是用来提升权限攻击攻击是指由威胁源所实施的、导致安全事件发生的行为,它是 漏洞利用 和 实现威胁 的过程,一旦攻击得手即会造成影响。
安全策略
安全策略是指在某个安全区域内,所有与安全活动相关的一套规则,它声明哪些行为是能做的、被
允许的,哪些行为是不能做的、被禁止的。这些规则是由此安全区域中所设立的一个安全权利机构
建立的,并由安全控制机构来描述、实施或实现的社会工程学。
安全机制
安全机制是一种用于解决和处理某种安全问题的方法,通常分为预防、检测和恢复三种类型。网络
安全中绝大多数安全服务和安全机制都是建立在密码技术的基础之上的,它们通过密码学方法对数
据信息进行加密和解密来实现网络安全的目标要求。
社会工程学
信息安全可以分为 Soft Security 和 Hard Security 两个部分。所谓的 “ 硬安全 ” ,主要就是具体的安全
IT 技术(比如:防火墙、入侵检测、漏洞扫描、抗拒绝服务 …… ),这些东西都是专家安全公司在搞,离绝大多数的读者可能比较遥远。而“ 软安全 ” 主要涉及管理、心理学、文化、人际交往等方
面,与具体的 IT 技术可能没有关系。今天所说的 “ 社会工程学 ” ,实际上就是 “ 软安全 ” ,如果你看过
电影《没有绝对的安全》的话,电影中主人公没有花一分钱搞到了肯德基的一份午餐就是利用社会
工程学的典型例子。
通俗地讲,社会工程学就是:利用人性之中的弱点(贪婪、恐惧、性欲…… )等心理学上的弱点来
影响别人,最终达到自己不可告人的目的。
APT
APT 是黑客以窃取核心资料为目的,针对客户所发动的网络攻击和侵袭行为,是一种蓄谋已久的 “ 恶意商业间谍威胁” 。这种行为往往经过长期的经营与策划,并具备高度的隐蔽性。 APT 的攻击手法,在于隐匿自己,针对特定对象,长期、有计划性和组织性地窃取数据,这种发生在数字空间的偷窃资料、搜集情报的行为,就是一种“ 网络间谍 ” 的行为。
APT 攻击是一个集合了多种常见攻击方式的综合攻击。综合多种攻击途径来尝试突破网络防御,通
常是通过 Web 或电子邮件传递,利用应用程序或操作系统的漏洞,利用传统的网络保护机制无法提
供统一的防御。除了使用多种途径,高级定向攻击还采用多个阶段穿透一个网络,然后提取有价值
的信息,这使得它的攻击更不容易被发现。
卡巴斯基遭 APT 攻击,全球知名网络安全公司卡巴斯基实验室遭遇 APT 攻击长达数月未察觉,实施
攻击的病毒 Duqu2.0 是现金为止最为复杂的蠕虫病毒,被广泛应用与各种 APT 攻击事件中。
2.为什么会出现网络安全问题?
网络的脆弱性
网络环境的开放性
“ INTERNET 的美妙之处在于你和每个人都能互相连接 , INTERNET 的可怕之处在于每个人都能和你互相连接 ”
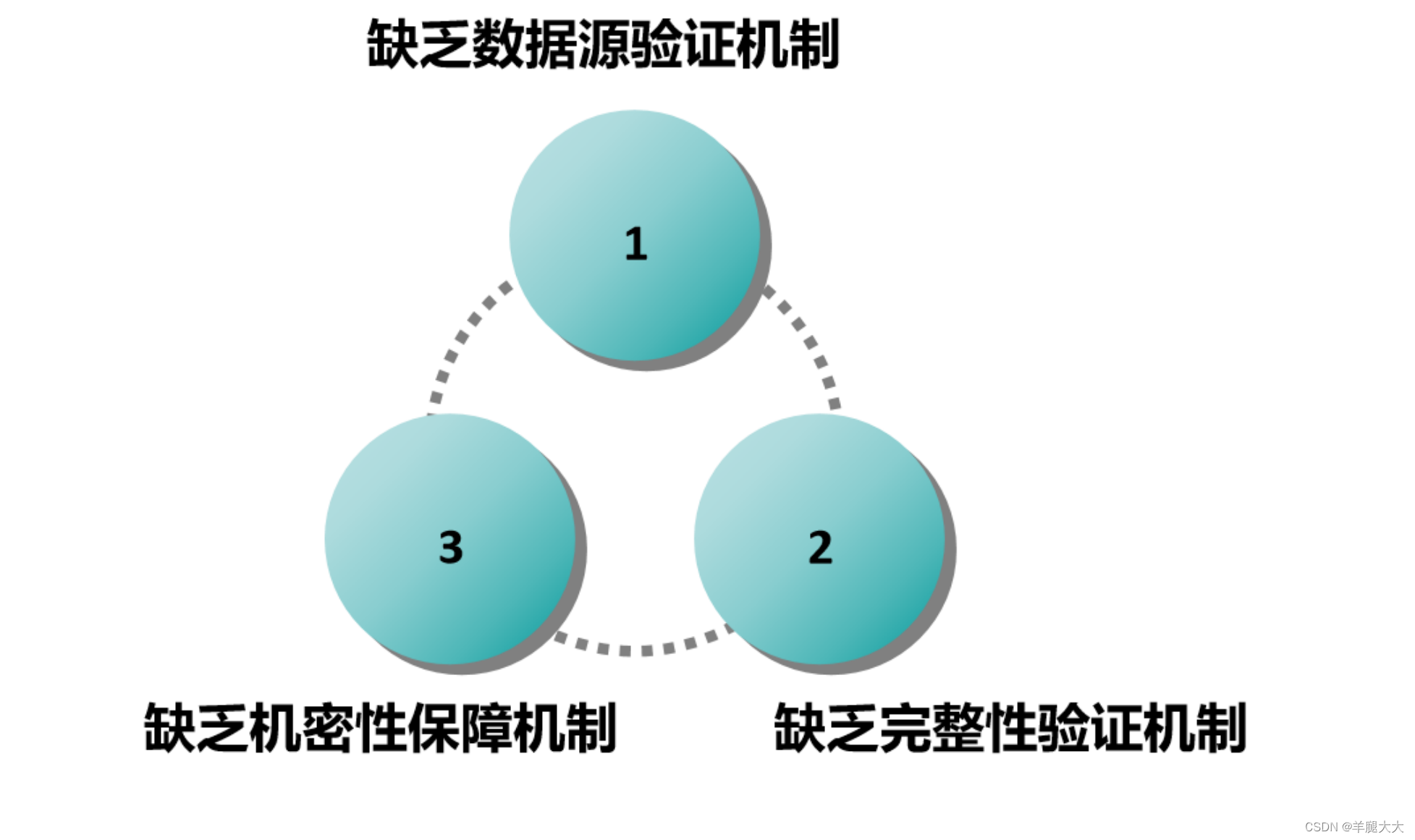
协议栈自身的脆弱性
TCP/IP 协议族是使用最广泛的网络互连协议。但由于协议在设计之初对安全考虑的不够,导致协议存在着一些安全风险问题。Internet 首先应用于研究环境,针对少量、可信的的用户群体,网络安全问题不是主要的考虑因素。因此,在TCP/IP 协议栈中,绝大多数协议没有提供必要的安全机制,例如:
- 不提供认证服务
- 明码传输,不提供保密性服务,不提供数据保密性服务
- 不提供数据完整性保护不提供抗抵赖服务
- 不保证可用性——服务质量(QoS)

操作系统自身的漏洞
人为原因
在程序编写过程中,为实现不可告人的目的,在程序代码的隐藏处保留后门。
客观原因
受编程人员的能力,经验和当时安全技术所限,在程序中难免会有不足之处,轻则影响程序效率,
重则导致非授权用户的权限提升。
硬件原因
由于硬件原因,使编程人员无法弥补硬件的漏洞,从而使硬件的问题通过软件表现。 缓冲区溢出攻击 缓冲区是内存中存放数据的地方。在程序试图将数据放到机器内存中的某一个位置的时候,因为没有足够的空间就会发生缓冲区溢出。而人为的溢出则是有一定企图的,攻击者写一个超过缓冲区长度的字符串,植入到缓冲区,然后再向一个有限空间的缓冲区中植入超长的字符串,这时可能会出现两个结果:
- 一是过长的字符串覆盖了相邻的存储单元,引起程序运行失败,严重的可导致系统崩溃;
- 另一个结果就是利用这种漏洞可以执行任意指令,甚至可以取得系统root特级权限。

缓冲区溢出攻击原理
- 缓冲区溢出攻击利用编写不够严谨的程序,通过向程序的缓冲区写入超过预定长度的数据,造成缓存的溢出,从而破坏程序的堆栈,导致程序执行流程的改变
缓冲区溢出的危害
终端的脆弱性及常见攻击
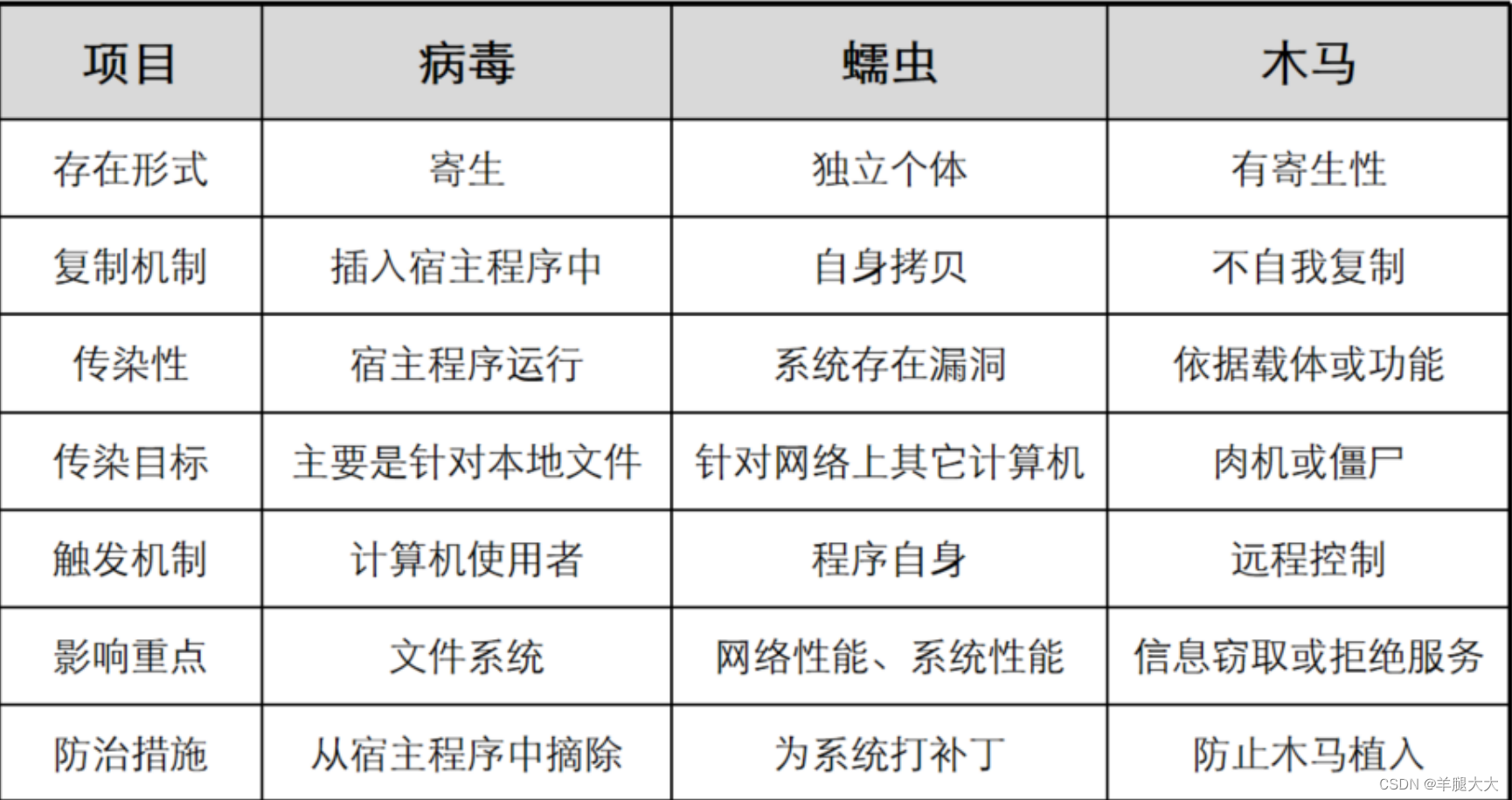
终端是占据企业数量最多的计算机系统,容易遭受计算机病毒为代表的恶意代码的攻击。
常见的恶意代码包括:
 其他攻击
其他攻击
社工攻击
原理:
社会工程攻击,是一种利用 " 社会工程学 " 来实施的网络攻击行为。
在计算机科学中,社会工程学指的是通过与他人的合法地交流,来使其心理受到影响,做出某些动作或者是透露一些机密信息的方式。这通常被认为是一种欺诈他人以收集信息、行骗和入侵计算机系统的行为。
防御手段:
定期更换各种系统账号密码,使用高强度密码等
人为因素
无意的行为
- 工作失误——如按错按钮;
- 经验问题——不是每个人都能成为系统管理员,因此并不了解贸然运行一个不知作用的程序时会怎么样;
- 体制不健全——当好心把自己的账号告诉朋友时,你却无法了解他会如何使用这一礼物;
恶意的行为
- 出于政治的、经济的、商业的、或者个人的目的
- 病毒及破坏性程序、网络黑客
- 在Internet上大量公开的攻击手段和攻击程序。
防范措施
- 提升安全意识,定期对非IT人员进行安全意识培训和业务培训;
- 设置足够强的授权和信任方式,完善最低权限访问模式;
- 组织需要完善和落地管理措施,保障安全管理制度是实际存在的;
- 善于利用已有的安全手段对核心资产进行安全保护等
拖库、洗库、撞库
原理:
拖库:是指黑客入侵有价值的网络站点,把注册用户的资料数据库全部盗走的行为。
洗库:在取得大量的用户数据之后,黑客会通过一系列的技术手段和黑色产业链将有价
值的用户数据变现,这通常也被称作洗库。
最后黑客将得到的数据在其它网站上进行尝试登陆,叫做撞库,因为很多用户喜欢使用
统一的用户名密码。
防御手段:
重要网站 /APP 的密码一定要独立 、电脑勤打补丁,安装一款杀毒软件、尽量不使用 IE 浏
览器、使用正版软件、不要在公共场合使用公共无线做有关私密信息的事、自己的无线
AP ,用安全的加密方式(如 WPA2 ),密码复杂些、电脑习惯锁屏等。
跳板攻击
原理:
攻击者通常并不直接从自己的系统向目标发动攻击,而是先攻破若干中间系统 , 让它们成
为 “ 跳板 ” ,再通过这些 “ 跳板 ” 完成攻击行动。
跳板攻击就是通过他人的计算机攻击目标 . 通过跳板实施攻击。
防御手段:
安装防火墙,控制流量进出。系统默认不使用超级管理员用户登录,使用普通用户登
录,且做好权限控制。
钓鱼攻击/鱼叉式钓鱼攻击
原理:
钓鱼式攻击是一种企图从电子通讯中,通过伪装成信誉卓著的法人媒体以获得如用户
名、密码和信用卡明细等个人敏感信息的犯罪诈骗过程。
鱼叉式网络钓鱼指针对特定目标进行攻击的网络钓鱼攻击。
防御手段:
保证网络站点与用户之间的安全传输,加强网络站点的认证过程,即时清除网钓邮件,
加强网络站点的监管。
水坑攻击
原理:
攻击者首先通过猜测(或观察)确定特定目标经常访问的网站,并入侵其中一个或多个
网站,植入恶意软件。最后,达到感染目标的目的。
防御手段:
在浏览器或其他软件上,通常会通过零日漏洞感染网站。
针对已知漏洞的防御措施是应用最新的软件修补程序来消除允许该网站受到感染的漏洞。用户监控可以帮助确保他们的所有软件都运行最新版本。如果恶意内容被检测到,运维人员可以监控他们的网站和网络,然后阻止流量。
3.什么样的网络是安全的?
网络安全的目的

网络安全要素
- 保密性—confidentiality
- 完整性—integrity
- 可用性—availability
- 可控性—controllability
- 不可否认性—Non-repudiation
- 保密性(confidentiality)与Integrity(完整性)和 Availability(可用性)并称为信息安全的CIA三要素。
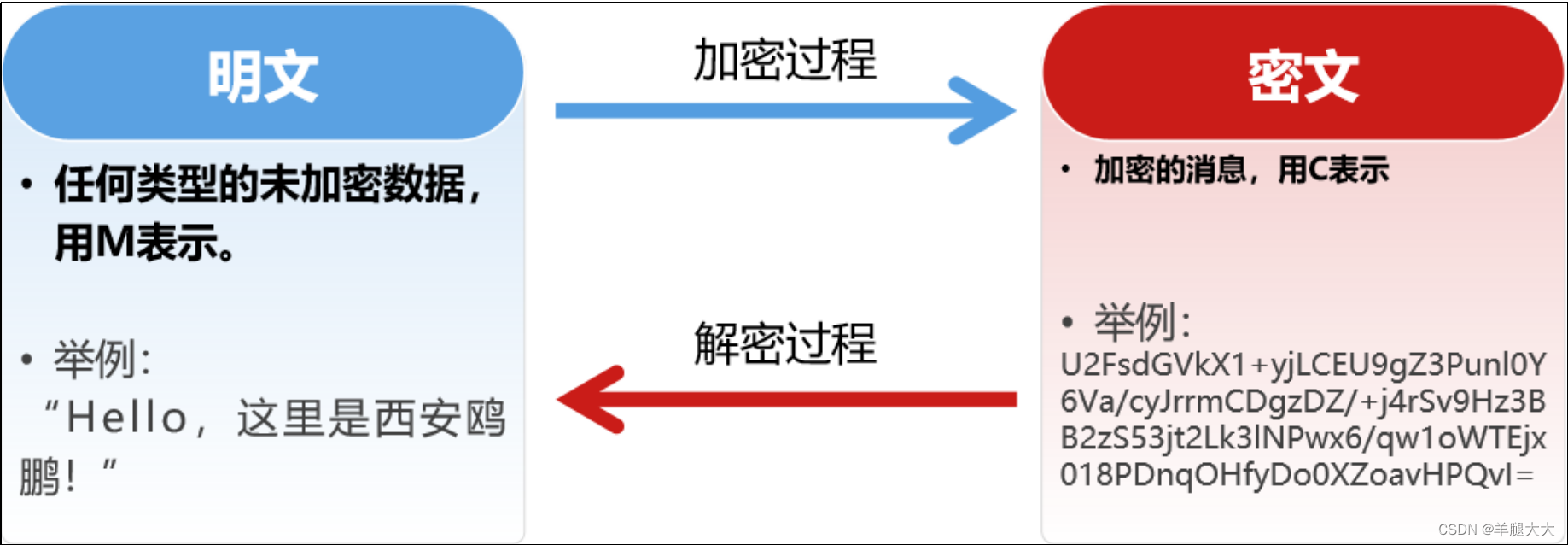
保密性
- 保密性:确保信息不暴露给未授权的实体或进程。
- 目的:即使信息被窃听或者截取,攻击者也无法知晓信息的真实内容。可以对抗网络攻击中的被动
- 攻击。
完整性
- 只有得到允许的人才能修改实体或进程,并且能够判别出实体或进程是否已被修改。完整性鉴别机制,保证只有得到允许的人才能修改数据 。可以防篡改。
可用性
- 得到授权的实体可获得服务,攻击者不能占用所有的资源而阻碍授权者的工作。用访问控制机制,阻止非授权用户进入网络。使静态信息可见,动态信息可操作,防止业务突然中断。

doss攻击:拒绝式服务攻击,就是破坏可用性。
可控性
可控性主要指对危害国家信息(包括利用加密的非法通信活动)的监视审计。控制授权范围内的信
息流向及行为方式。使用授权机制,控制信息传播范围、内容,必要时能恢复密钥,实现对网络资
源及信息的可控性。
不可否认性
不可否认性:对出现的安全问题提供调查的依据和手段。使用审计、监控、防抵赖等安全机制,使
得攻击者、破坏者、抵赖者 “ 逃不脱 " ,并进一步对网络出现的安全问题提供调查依据和手段,实现
信息安全的可审查性。

信息安全的五要素案例

威胁模型
所谓的网络安全威胁是指可能破坏某一网络资源的机密性、完整性以及可用性等安全基本要素的来源或原因。例如对于数据库中的数据来说, SQL 注入攻击就是一种网络威胁。一旦攻击得手,被攻击者就可能会被窃取机密数据从而导致数据的机密性被破坏。
使用 威胁模型分析 (Threat Model Analysis, TMA) 可以帮助确定产品、应用程序、网络或环境中存在的风险和可能的攻击路径。TMA 的目标是确定哪些威胁需要缓解以及如何缓解。具体来说,威胁模型对于帮助企业应对安全威胁具有五个方面的具体作用:
1. 评估风险更加有效。传统的风险评估定级方法是按照通用的安全管理框架和标准(如 ISO 27001 )进行操作,但实际结果存在发布的标准不适应新情况、规定的措施不够深入等问题,威胁模型分析可以弥补照搬安全行业标准进行管理所带来的缺陷。
2. 帮助深入理解企业系统。威胁模型的建立要求对企业内部的信息系统资产进行评估,对各个子系统
之间的支持配合方式做深入详细的了解。使用威胁模型进行安全管理有助于深入理解整个企业系
统。
3. 提高相关员工安全意识。在建立安全模型过程中,为深入了解系统功能和运行情况,需要与企业中的工作人员进行沟通,在此过程中有助于系统使用者树立起更好的安全意识,以便在以后的运维和管理工作中更加严谨和规范。
4. 安全管理措施次序优化。威胁模型可以帮助企业摒弃通用的、泛泛的管理措施,结合企业自身具体情况,着眼于可能面临的具体风险,选择合理的、有针对性的、有效的安全管理措施并优化其次
序。
5. 提高安全管理效率。安全评估在时间上是受限的,因此必须把有限的时间集中在值得关注的点上。
威胁模型可以让企业的安全管理人员更加透彻的理解各种攻击方式,从而明白真正具有威胁的攻击
路径,避免无意义的时间消耗。
当前普遍采用的威胁模型包括:微软 STRIDE 模型、微软 DREAD 模型、卡耐基梅隆大学的 OCTAVE 模型等。威胁模型是多种多样的,但是建立过程却大致相同,基本上可以分为四个步骤,分别是:明确目标、分解系统、识别威胁、评估威胁。
STRIDE模型是由微软公司提出的一种信息安全威胁建模方法,用于帮助识别和评估计算机系统和软件应用程序中的潜在安全威胁。该模型的目的是帮助开发人员和安全专家在设计和开发阶段识别可能的攻击路径和漏洞,从而在系统投入使用前采取相应的安全措施。
微软 STRIDE 模型
STRIDE模型是一个缩写,表示以下六种常见的信息安全威胁:
-
Spoofing (伪装): 攻击者伪装成合法用户、设备或系统来获取未授权的访问权限。
-
Tampering (篡改): 攻击者篡改数据、代码或配置信息,以破坏系统的完整性或导致不正确的运行。
-
Repudiation (抵赖): 攻击者试图否认自己的行为,通常通过删除或修改日志和审计信息来隐藏攻击痕迹。
-
Information Disclosure (信息泄露): 攻击者未经授权地访问、获取或披露敏感信息。
-
Denial of Service (拒绝服务): 攻击者通过向系统发送大量请求或利用系统漏洞来使系统过载或崩溃,导致合法用户无法访问。
-
Elevation of Privilege (提权): 攻击者通过利用系统漏洞或安全弱点获取未经授权的权限,从而执行特权操作。
4.漏洞管理相关标准
漏洞标准是关于漏洞命名、评级、检测、管理的一系列规则和规范,是信息安全保障体系的重要组成部
分,是对漏洞进行合理、有效管控的重要手段,为信息安全测评和风险评估提供了基础。
美国的安全研究机构与组织先后推出了一系列有影响力的标准,其中, CVE 、 CVSS 等 7 个标准已被国
际电信联盟( ITU )的电信标准化部门( ITU-T )纳入到了其 X 系列(数据网、开放系统通信和安全性)
建议书中,成为了 ITU-T 推荐的国际漏洞标准。如下表格列出了这 7 个标准及其建议书编号:
-
CVE (Common Vulnerabilities and Exposures): CVE是一个公共漏洞识别系统,为已知漏洞分配唯一的标识符。每个CVE标识符都用于标识一个特定的漏洞,以便不同的组织和厂商能够在其产品和系统中追踪和处理漏洞。
-
CVSS (Common Vulnerability Scoring System): CVSS是一种用于评估漏洞严重性的开放式标准。CVSS提供了一种公认的方法来对漏洞进行评分,帮助组织优先处理最严重的漏洞。
-
ISO/IEC 27001: ISO/IEC 27001是一项信息安全管理标准,其中包含了漏洞管理作为一个重要组成部分。该标准强调建立和实施信息安全管理体系(ISMS),包括对漏洞的识别、评估和响应措施。
-
NIST SP 800-53: 由美国国家标准与技术研究所(NIST)发布的SP 800-53是一份广泛应用的信息安全控制目录,其中包含了漏洞管理的最佳实践和指导。
-
ISO/IEC 29147: ISO/IEC 29147是一项用于漏洞披露的国际标准。该标准规定了漏洞披露的流程和原则,以促进负责任的漏洞披露和协调。
-
ISO/IEC 30111: ISO/IEC 30111是一项用于漏洞披露的国际标准,强调在漏洞披露中的相互信任和协作。
-
OWASP (Open Web Application Security Project): OWASP是一个致力于提供开放式Web应用安全项目的国际性组织。其提供了一系列关于漏洞管理和应对的指南和最佳实践。
-
SANS Critical Security Controls: SANS关键安全控制是一组重要的安全措施,其中包含了漏洞管理的最佳实践和建议。
为了实现「可度量的安全」和「可执行的安全」标准,除了上述 7 个标准之外还有一些相关安全标准被
设计提出。例如:威胁情报领域的威胁情报交换格式标准 STIX 、恶意软件分类和特征标准 MAEC 和可
扩展配置检查清单描述标准 XCCDF 等。这些标准在公布之后并非一成不变,有些标准在发展的过程中被
整合到其他相关标准之中。例如: CybOX 就已经被整合到了 STIX 2.0 标准之中。
借用这些标准的主要制定者 mitre.org 的一张图来概括这些标准在「安全测量」和「安全管理」架构中
所扮演的角色,如下图所示: 
4.防火墙是什么
20 世纪 90 年代,随着互联网的普及,出现了路由器访问控制列表无法抵御的攻击和非法访问等一系列威胁,因此出现了针对这些威胁的防范策略需求。1992 年 OECD 组织发布了 “ 信息系统安全指导书 ", 其中定义了为构建安全网络体系而需要遵循的CIA 基本理念。 CIA 是机密性 (Confidentiality) 、完整性(Integrity)、可用性(Availability)三个英文单词的首字母组合,这三个方面的主要威胁及其对策如下: 
路由交换终归结底是连通性设备。
- 网络在远古时期没有防火墙大家都是联通的,any to any。
防火墙
防御对象:
- 授权用户
- 非授权用户
- 防火墙是一种隔离(非授权用户在区域间)并过滤(对受保护网络有害流量或数据包)的设备。
防火墙的区域:
包过滤防火墙 ---- 访问控制列表技术 --- 三层技术
代理防火墙 ---- 中间人技术 --- 应用层
- 降低包过滤颗粒度的一种做法,区域之间通信使用固定设备。
- 代理技术只能针对特定的应用来实现,应用间不能通用。
- 技术复杂,速度慢
- 能防御应用层威胁,内容威胁
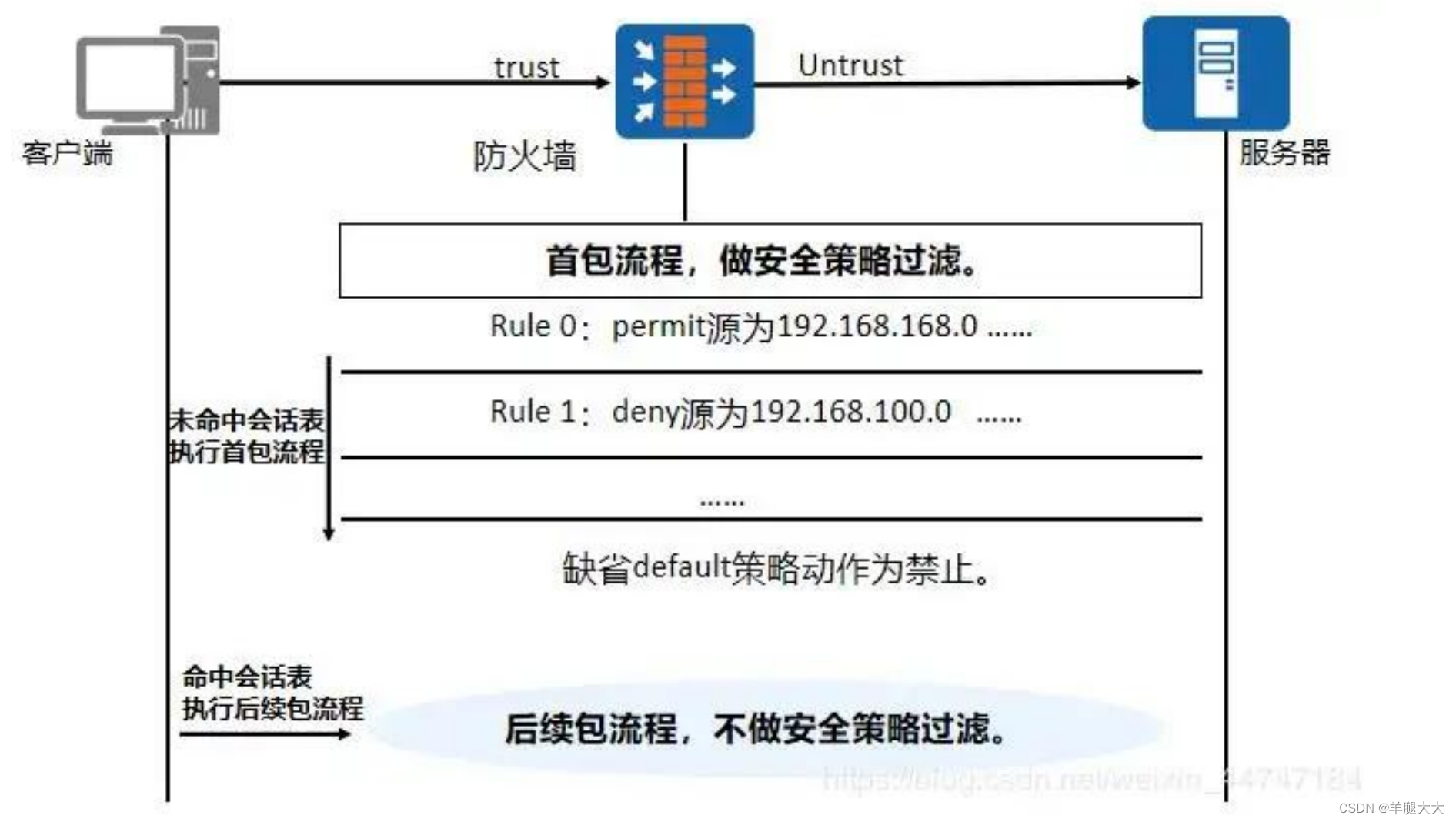
状态防火墙 --- 会话追踪技术 --- 三层、四层
- 在包过滤(ACL表)的基础上增加一个会话表,数据包需要查看会话表来实现匹配。
- 会话表可以用hash来处理形成定长值,使用CAM芯片处理,达到交换机的处理速度。
- 首包机制
- 细颗粒度
- 速度快
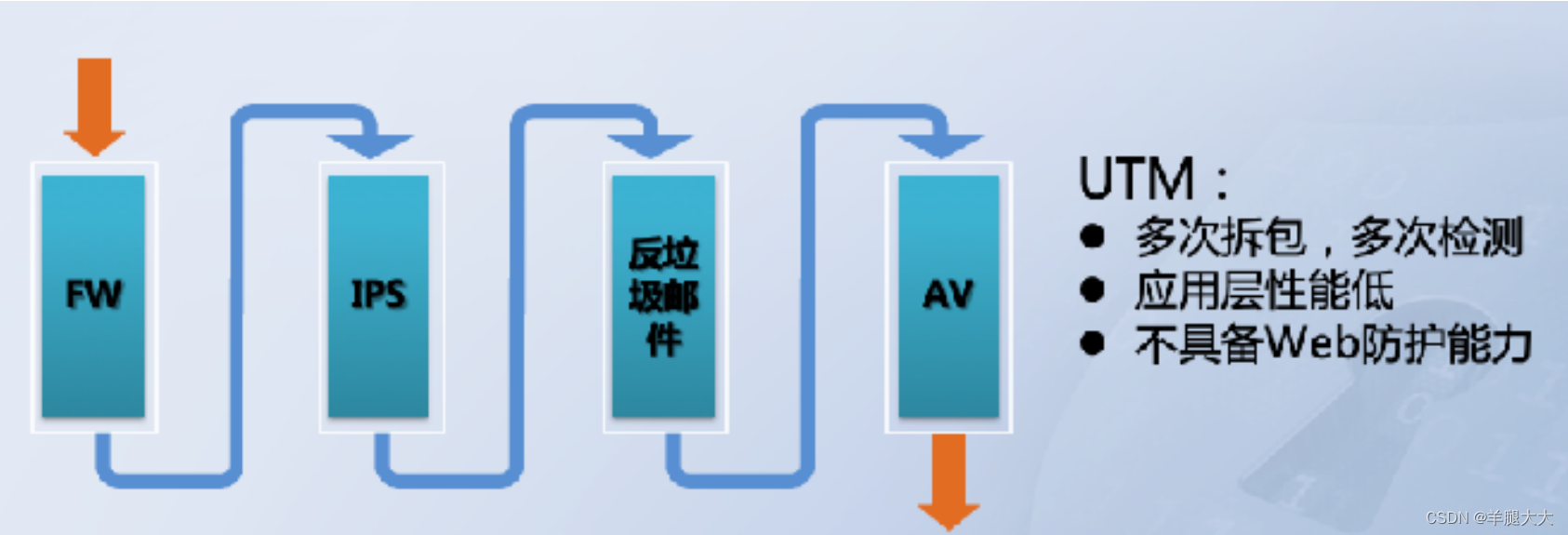
UTM--- 深度包检查技术 ---- 应用层
- 把应用网关和IPS等设备在状态防火墙的基础上进行整合和统一。
- 把原来分散的设备进行统一管理,有利于节约资金和学习成本
- 统一有利于各设备之间协作。
- 设备负荷较大并且检查也是逐个功能模块来进行的,貌合神离,速度慢。
下一代防火墙
2008 年 Palo Alto Networks 公司发布了下一代防火墙( Next-Generation Firewall ),解决了多个功能同时运行时性能下降的问题。同时,下一代防火墙还可以基于用户、应用和内容来进行管控。2009 年Gartner(一家 IT 咨询公司) 对下一代防火墙进行了定义,明确下一代防火墙应具备的功能特性。 Gartner把 NGFW 看做不同信任级别的网络之间的一个线速( wire-speed )实时防护设备,能够对流量执行深度检测,并阻断攻击。Gartner 认为, NGFW 必须具备以下能力:
1. 传统防火墙的功能
NGFW 是新环境下传统防火墙的替代产品,必须前向兼容传统防火墙的基本功能,包括包过滤、协议状态检测、NAT 、 VPN 等。
2. IPS 与防火墙的深度集成 NGFW 要支持 IPS 功能,且实现与防火墙功能的深度融合,实现 1+1>2 的效果。 Gartner 特别强调 IPS 与防
火墙的 “ 集成 ” 而不仅仅是 “ 联动 ” 。例如,防火墙应根据 IPS 检测到的恶意流量自动更新下发安全策略,而不需要管理员的介入。换言之,集成IPS 的防火墙将更加智能。 Gartner 发现, NGFW 产品和独立 IPS 产品的市场正在融合,尤其是在企业边界的部署场景下,NGFW 正在吸收独立 IPS 产品市场。
3. 应用感知与全栈可视化
具备应用感知能力,并能够基于应用实施精细化的安全管控策略和层次化的带宽管理手段,是 NGFW 引进的最重要的能力。传统的状态检测防火墙工作在二到四层,不会对报文的载荷进行检查。NGFW 能对七层检测,可以清楚地呈现网络中的具体业务,并实行管控。
4. 利用防火墙以外的信息,增强管控能力
防火墙能够利用其他 IT系统提供的用户信息、位置信息、漏洞和网络资源信息等,帮助改进和优化安全策略。例如,通过集成用户认证系统,实现基于用户的安全策略,以应对移动办公场景下,IP地址变化带来的管控难题。 



 其他攻击
其他攻击