做网站该注意哪些基本要素如何免费制作网站
官网下载visual studio,社区版免费的
https://visualstudio.microsoft.com/zh-hans/
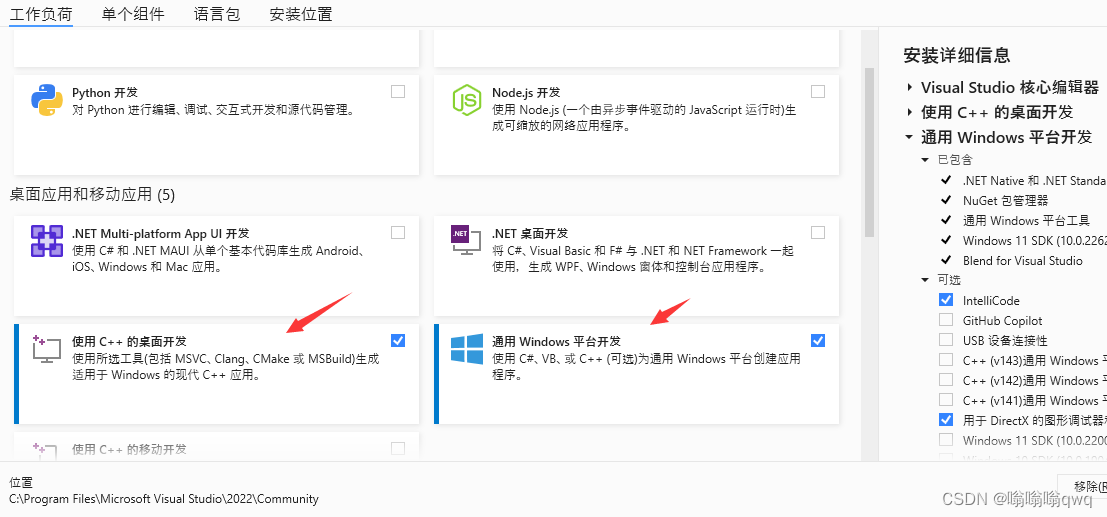
下载好以后选择自己的需求进行安装,我选择了两个,剩下的是默认。
创建文件:
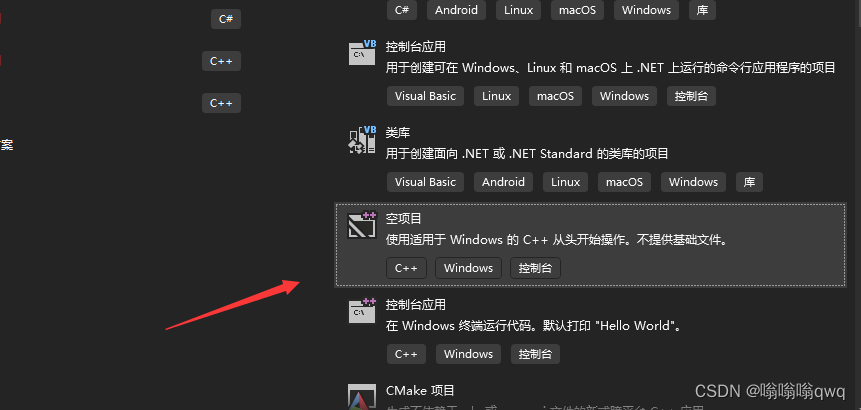
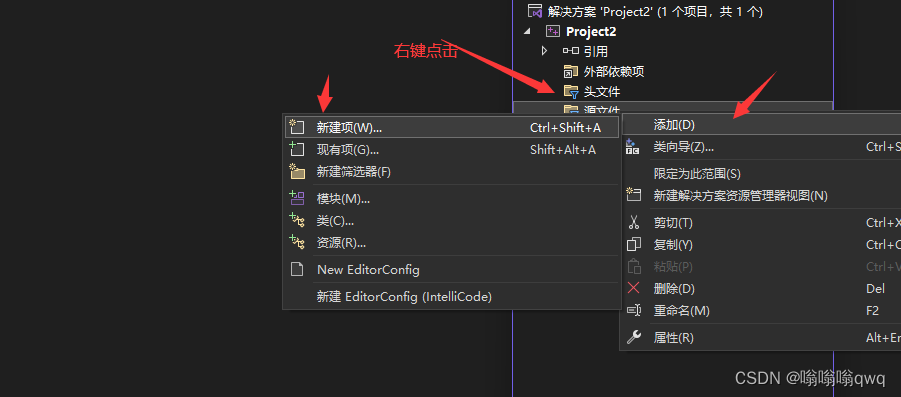
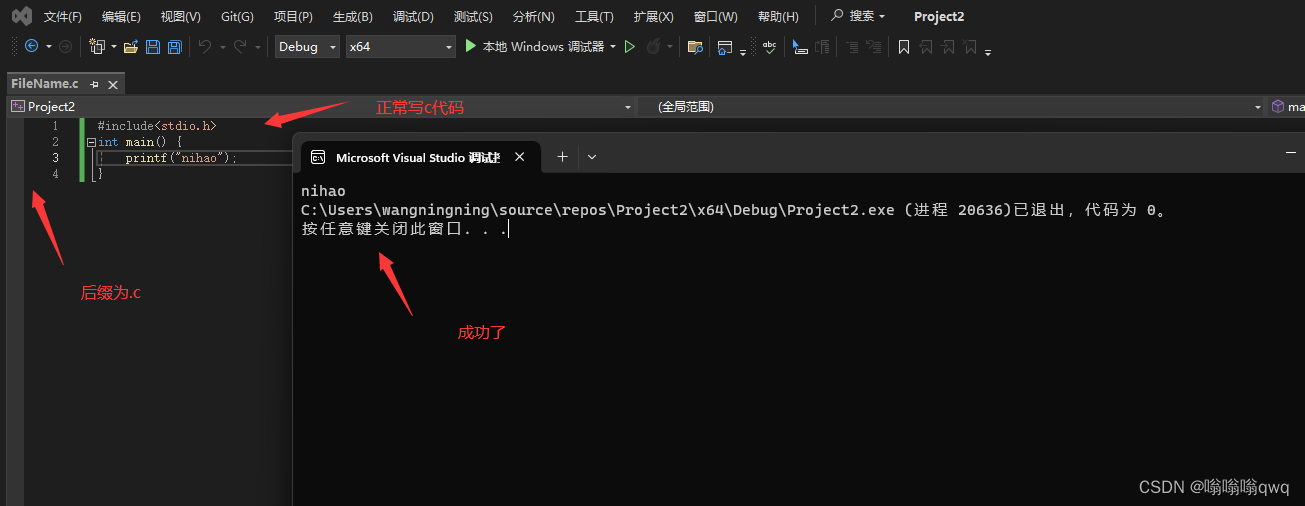
官网下载visual studio,社区版免费的
https://visualstudio.microsoft.com/zh-hans/

下载好以后选择自己的需求进行安装,我选择了两个,剩下的是默认。

创建文件:


