如何做网站的实时画面口碑营销名词解释
代码地址: GitHub - 137/gorm-sharding: Sharding 是一个高性能的 Gorm 分表中间件。它基于 Conn 层做 SQL 拦截、AST 解析、分表路由、自增主键填充,带来的额外开销极小。对开发者友好、透明,使用上与普通 SQL、Gorm 查询无差别.解决了原生sharding的三个问题:1.不支持不带分表键的查询 2,不支持不同分表策略的配置 3.没有配置分表的自定义sql可能因为无法解析而发生异常
更新点
💡
原生gorm-sharding支持的功能有限,在公共包common中做了功能的扩展
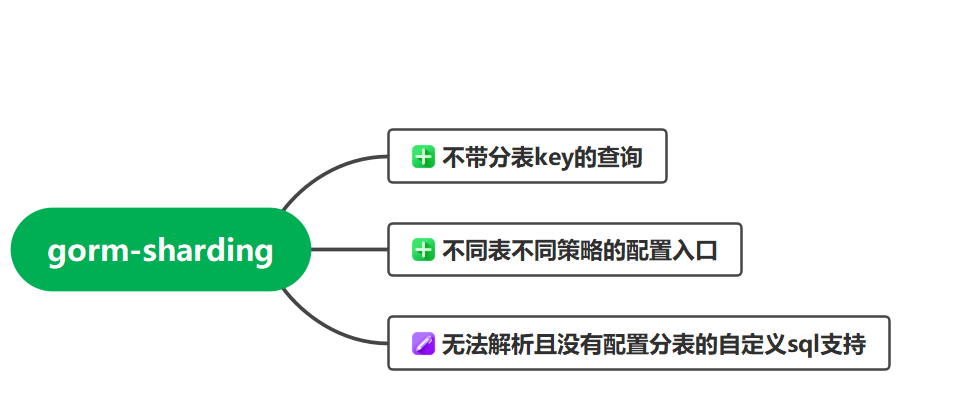
- 本插件的gorm版本与现在的大部分服务一致v1.20.8,与原作者的不一致,避免版本冲突
- 原sharding解析sql用的sqlParse不一定能成功解析一些自定义的复杂sql,所以遇到解析不了的直接扔给gorm处理。如果涉及到分表的则需改成可以被sharding识别的标准gorm sql写法
- 原sharding本身不支持全表扫描,在此做了支持
- 原sharding不支持全表汇总查询,在此做了对count和sum的支持
- 原sharding不支持多分表配置不同分表策略,在此增加了配置接口
简要
Gorm Sharding 插件使用 SQL 解析器和替换将大表拆分为较小的表,将查询重定向到分片表。给您高性能的数据库访问。
Gorm Sharding 是一个高性能的数据库分表中间件。
它基于Conn层做SQL拦截、AST解析、分表路由、自增主键填充,带来的额外费用极小。对开发者友好、透明,使用上与普通SQL、Gorm查询无差别,只需要额外注意一下分表键条件。
注意事项
- 1.不要自己拼接sql会导致无法识别分表键,目前解析的是gorm条件表达式,而不是sql树(binaryTree),所以无法支持原生sql的分表 建议写法.where().orderby().limit().offset().find这样子
- 2.查询条件需要分表键,如果没有的话需要UnionFlag 配置为true才不会报错,但是会导致全表扫描,慎用
特征
- 非侵入式设计。加载插件,指定配置,一切就完成了。
- 快如闪电。没有基于网络的中间件,与 Go 一样快。
- 多种数据库(PostgreSQL、MySQL)支持。
- 集成主键生成器(Snowflake、PostgreSQL 序列、自定义等)。
快速上手
1. go mod引入
2. gorm插件加载
shardByOrderIdConf := gormsharding.Config{ShardingKey: "order_id",NumberOfShards: uint(shardingNumber),PrimaryKeyGenerator: gormsharding.PKCustom, PrimaryKeyGeneratorFn: func(_ int64) int64 {return 0},ShardingAlgorithm: func(value any) (suffix string, err error) {if orderId, ok := value.(string); ok {return fmt.Sprintf("_%04d", HashStr(orderId)%shardingNumber), nil}return "", errors.New("invalid orderId")},ShardingAlgorithmForUnion: func(tableId int) (suffix string, err error) {return fmt.Sprintf("_%04d", tableId), nil},UnionFlag: true,}db.Use(gormsharding.RegisterMultiConf(map[string]gormsharding.Config{"order": shardByOrderIdConf,}))原始代码加载方式:
//分表中间件DBHandle.Use(sharding.Register(sharding.Config{ShardingKey: ShardingKey,NumberOfShards: ShardingNumber,//PrimaryKeyGenerator: sharding.PKMySQLSequence,PrimaryKeyGenerator: sharding.PKCustom,PrimaryKeyGeneratorFn: func(_ int64) int64 {return 0},}, ShardTablesByUid...))dao层调用
尽量采用gorm的标准写法,避免使用原生sql,可能导致无法分表
示例代码
orm := dao.GetKpayDB()db := orm.DBHandle.Table("order")if order.Uid != 0 {db = orm.DBHandle.Table("uid_order")}getOrderCondition(order, db)db = db.Order(" create_tm desc ")if order.CurPage > 0 && order.PageSize > 0 {db = db.Limit(order.PageSize).Offset((order.CurPage - 1) * order.PageSize)}err = db.Find(&orders).Errorif err != nil && err != gorm.ErrRecordNotFound {_ = log.Error(nil, fmt.Sprintf("GetOrders error, err=%v", err))return}工作原理
原理图
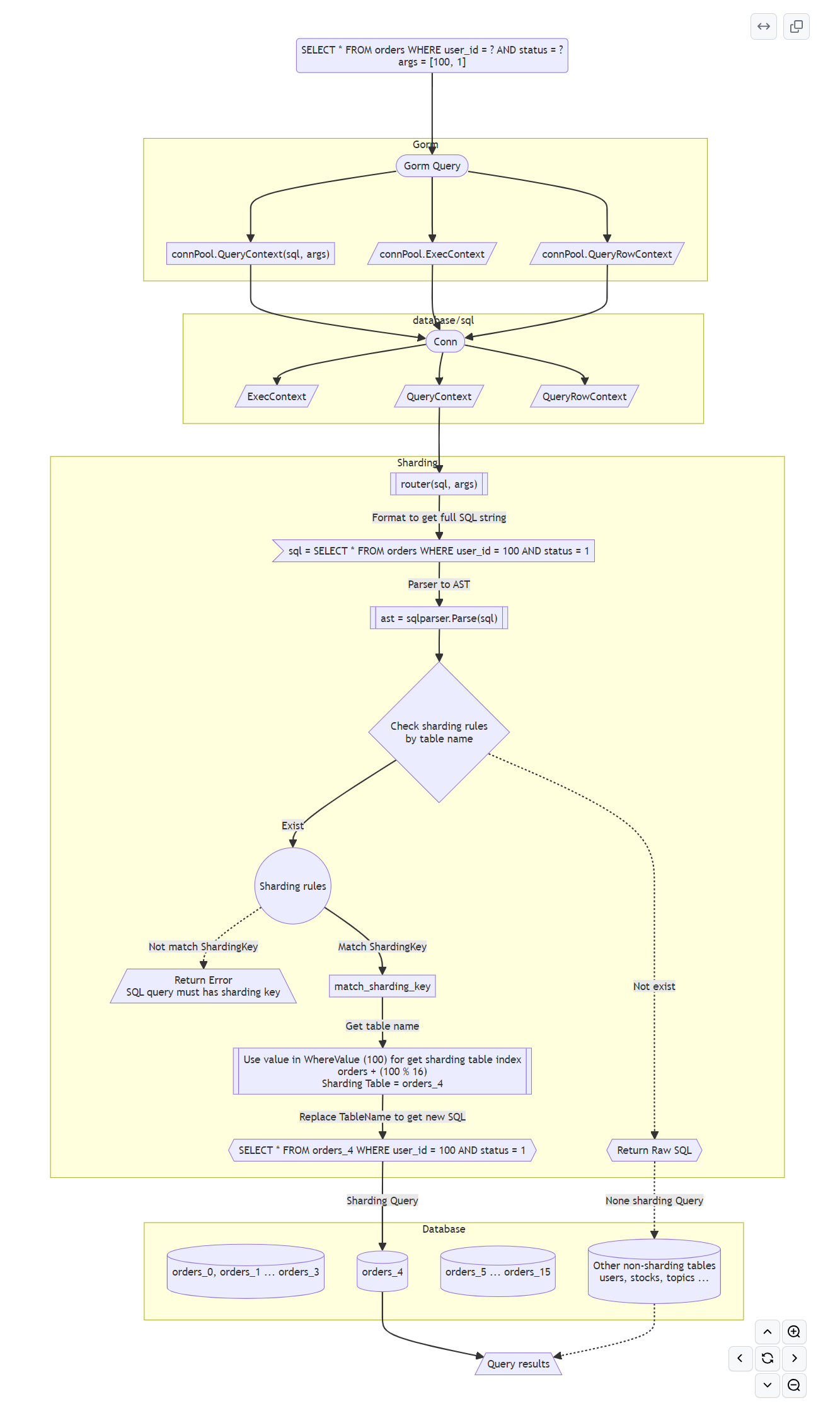
插件加载
Sharding实现了gorm接口
// Plugin GORM plugin interface
type Plugin interface {Name() stringInitialize(*DB) error
}Initialize中执行了函数compile
参数预处理(分表主键算法、后缀处理)Initialize中生成了gorm语句执行的钩子,switchConn主要处理双写的
func (s *Sharding) registerCallbacks(db *gorm.DB) {s.Callback().Create().Before("*").Register("gorm:sharding", s.switchConn)s.Callback().Query().Before("*").Register("gorm:sharding", s.switchConn)s.Callback().Update().Before("*").Register("gorm:sharding", s.switchConn)s.Callback().Delete().Before("*").Register("gorm:sharding", s.switchConn)s.Callback().Row().Before("*").Register("gorm:sharding", s.switchConn)s.Callback().Raw().Before("*").Register("gorm:sharding", s.switchConn)
}sharding实现gorm的接口
type ConnPool interface {PrepareContext(ctx context.Context, query string) (*sql.Stmt, error)ExecContext(ctx context.Context, query string, args ...interface{}) (sql.Result, error)QueryContext(ctx context.Context, query string, args ...interface{}) (*sql.Rows, error)QueryRowContext(ctx context.Context, query string, args ...interface{}) *sql.Row
}实现的接口中都会调用resolve的函数 (解决旧查询拆分为全表查询和分表查询)
配置参数说明
以下标红的是本包中新增的字段
- UnionFlag:
- 类型:布尔值
- 说明:表示是否启用联合查询标志。当为 true 时,即使没有分表键,也能够查询,但会扫描全表,需要注意性能问题。 建议配成false,暴露出没有分表键的查询
- DoubleWrite:
- 类型:布尔值
- 说明:表示是否启用双写功能。当启用时,数据将同时写入主表和分表中。
- ShardingKey:
- 类型:字符串
- 说明:指定用于分表的列名。例如,对于产品订单表,可以根据
user_id来分表。
- NumberOfShards:
- 类型:无符号整数
- 说明:指定分表的数量,即分表的个数
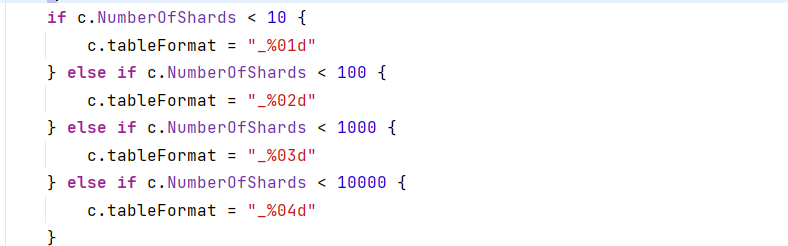
- tableFormat:
- 类型:字符串
- 说明:指定分表的表名格式。在不重写ShardingAlgorithm 分表函数时,自动根据分表数量算出
- ShardingAlgorithm:
- 类型:函数
- 说明:指定用于生成分表后缀的算法函数。该函数根据传入的列值,生成对应的分表后缀。
- ShardingAlgorithmForUnion:
- 类型:函数
- 说明:与
ShardingAlgorithm对应,用于处理全表扫描但无分表字段查询的情况。根据传入的表 ID,直接返回对应的分表后缀。
- ShardingSuffixs:
- 类型:函数
- 说明:生成所有分表后缀的函数,用于支持迁移器和生成主键。在compile插件的时候生成函数--根据函数ShardingAlgorithm拼接后缀
- ShardingAlgorithmByPrimaryKey:
- 类型:函数
- 说明:指定根据主键生成分表后缀的算法函数。当没有指定分表键时使用。
- PrimaryKeyGenerator:
- 类型:整数
- 说明:指定主键生成器算法,可选项有 PKSnowflake、PKPGSequence 和 PKCustom。
- PrimaryKeyGeneratorFn:
- 类型:函数
- 说明:指定生成主键的算法函数。当使用自动增量类似的生成器时,可以忽略
tableIdx参数。PrimaryKeyGenerator为 PKCustom时,直接返回0表示不做处理,让mysql自动递增
